A page on how to find the equation and how to graph real world applications of linear equations.
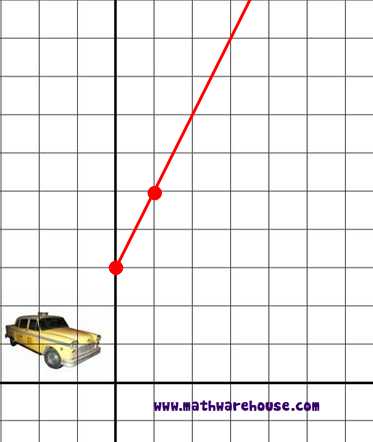
A cab company charges a $3 boarding rate in addition to its meter which is $2 for every mile. What is the equation of the line that represents this cab company's rate?

A cab company charges a $5 boarding rate in addition to its meter which is $3 for every mile. What is the equation of the line that represents this cab company's rate?
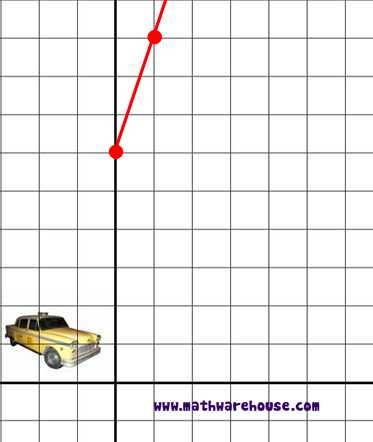
Slope of this line : 3
y-intercept of line: 5
Equation of this line(slope intercept form) : y = 3x +5
A cab company charges a $3 boarding rate in addition to its meter which is $½ for every mile. What is the equation of the line that represents this cab company's rate?
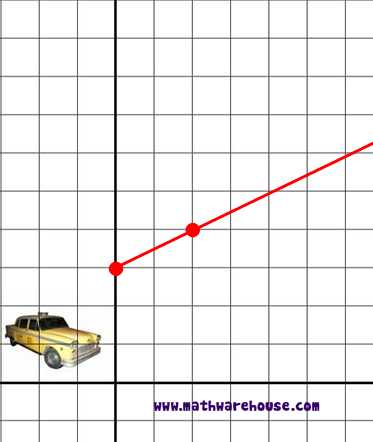
Slope of this line : ½
y-intercept of line: 3
Equation of this line(slope intercept form) : y = ½x +3
A cab company charges a $4 boarding rate in addition to its meter which is $ ¾ for every mile. What is the equation of the line that represents this cab company's rate?
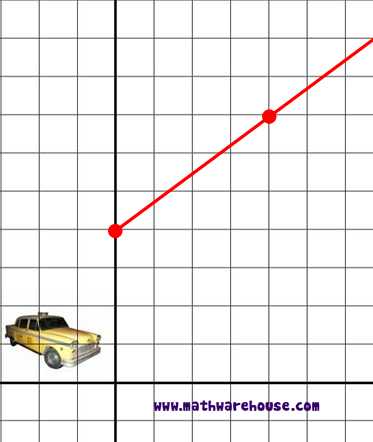
Slope of this line : ¾
y-intercept of line: 4
Equation of this line(slope intercept form) : y = ¾x + 4
A cab company does not charge a boarding fee but then has a meter of $4 an hour. What equation represents this cab company's rate?
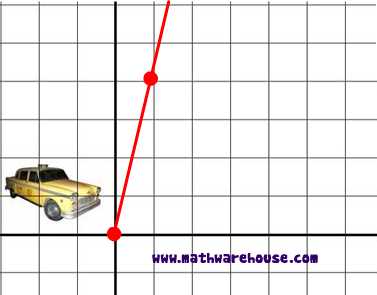
Slope of this line : 4
y-intercept of line: 0
Equation of this line(slope intercept form) : y = 4x